2025 AMC 8
Complete problem set with solutions and individual problem pages
Kei draws a -by- grid. He colors of the unit squares silver and the remaining squares gold. Kei then folds the grid in half vertically, forming pairs of overlapping unit squares. Let and equal the least and greatest possible number of gold-on-gold pairs, respectively. What is the value of ?
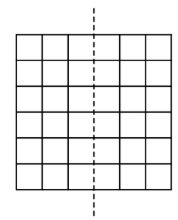
- A.
- B.
- C.
- D.
- E.
Solution 1
First, we note that there are "pairs" of squares folded on top of each other after the folding. The minimum number of gold pairs occurs when silver squares occupy the maximum number of pairs, and the maximum number of gold pairs occurs when silver squares occupy the minimum number of pairs. The latter case occurs when all silver squares are placed in different pairs, resulting in gold pairs. The former case occurs when the silver squares are paired up as much as possible, resulting in complete pairs and another square occupying another pair slot. Then there are gold pairs. Our answer is .
Solution 2
We can see that the least number of gold-on-gold pairs will be obtained when the silver squares are placed on the two sides so that they don't overlap when folded over (because then it will minimize the number of gold-on-golds). We can see that if we split them up and on both sides, and then fold it, the number of gold-on-golds will be .
The maximum number of gold-on-golds will be achieved when the silver squares overlap when folded over, which will increase the number of gold-on-golds. If we align 6 silver squares with each other on each side, and put the last one somewhere else, we get the maximum is . Therefore, the answer is .
