2025 AMC 8
Complete problem set with solutions and individual problem pages
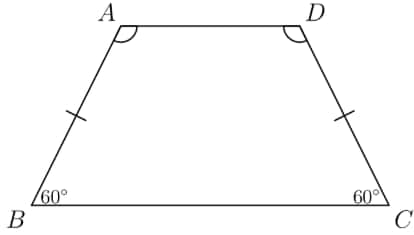
In trapezoid , angles and measure and . The side lengths are all positive integers, and the perimeter of is 30 units. How many non-congruent trapezoids satisfy all of these conditions?
- A.
- B.
- C.
- D.
- E.
Solution 1
Let be the length of the shorter base, and let be the length of the longer one. Note that these two parameters, along with the angle measures and the fact that the trapezoid is isosceles, uniquely determine a trapezoid. We drop perpendiculars down from the endpoints of the top base. Then the length from the foot of this perpendicular to either vertex will be half the difference between the lengths of the two bases, or . Now, since we have a 30-60-90 triangle and this side length corresponds to the "30" part, the length of the hypotenuse (one of the legs) is . Then the perimeter of the trapezoid is . The only other stipulation for this trapezoid to be valid is that (which was our assumption). We can now easily count the valid pairs , yielding . It is clear that proceeding further would cause , so we have valid trapezoids.
Solution 2
Let be the length of and , and let be the length of the shorter base. Because and , the length of the longer base is . Therefore, the perimeter is . The number of positive integer pairs is , meaning the answer is .
way where you don't have to test pairs:
We can rearrange to . We want to be a positive integer so b is a positive integer. 30 is a multiple of 3 and is just subtracting multiples of 3's from 30 so every number on the numerator of is a multiple of 3 under 30 ( is also a positive integer so it can't be larger than 30 or not be a multiple of 3). For to be divisible by 2 it must be even, so we are finding even multiples of 3 under 30 which are 24, 18, 12, and 6. Each number will give us a valid and a valid pair giving us 4 solutions.
