AMC 10 Daily Practice Round 2

Complete problem set with solutions and individual problem pages

Problem 20 Medium

Three diagonals are drawn in a regular hexagon of side length 1, splitting the hexagon into several regions. What is the least possible area of such a region?

  • A.

    \frac{\sqrt{3}}{24}

  • B.

    \frac{\sqrt{3}}{18}

  • C.

    \frac{\sqrt{3}}{16}

  • D.

    \frac{\sqrt{3}}{12}

  • E.

    \frac{\sqrt{3}}{8}

Answer:A

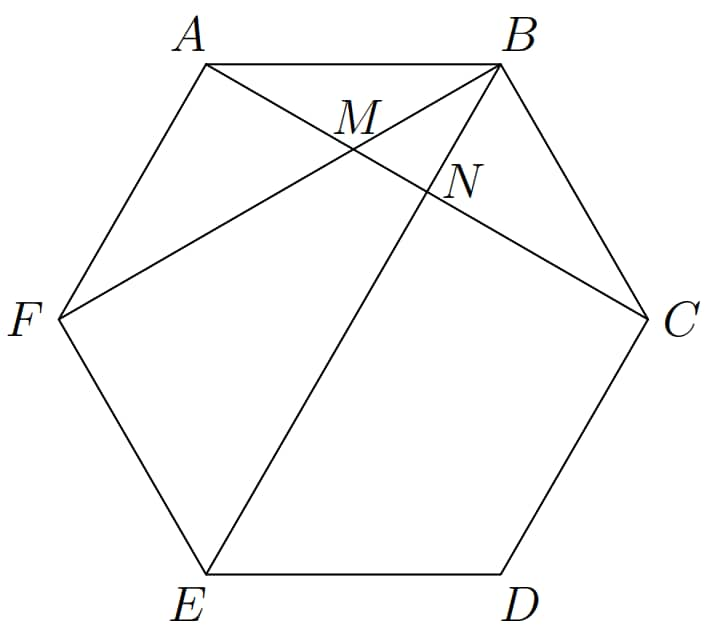
Above, the two diagonals stemming from a common vertex are \overline{B E} and \overline{B F}, which form the smallest angle possible of \angle E B F=30^{\circ}, and the third diagonal \overline{A C} bounds \angle E B F as tightly as possible.

The area we seek is A_{\triangle B M N}. First, triangles A B M and C F M are similar in ratio \frac{A B}{C F}=\frac{1}{2}, so \frac{A M}{C M}=\frac{1}{2} or, equivalently, \frac{A M}{A C}=\frac{1}{3}. Additionally, A N=C N by symmetry, which yields that \frac{C N}{A C}=\frac{1}{2}. Therefore, \frac{M N}{A C}=1-\frac{A M}{A C}-\frac{C N}{A C}=1-\frac{1}{3}-\frac{1}{2}=\frac{1}{6} . Now, triangles B M N and B A C share an altitude from B, implying \frac{A_{\triangle B M N}}{A_{\triangle B AC}}= \frac{M N}{A C}=\frac{1}{6}. Then, since \triangle A B C is a 30-30-120 triangle with leg length A B=1, it has area \frac{\sqrt{3}}{4}, giving us the requested answer of A_{\triangle B M N}=(\mathbf{A}) \frac{\sqrt{3}}{24}.

Related Problems
Problem 18 AMC 10 Daily Practice Round 2
Problem 19 AMC 10 Daily Practice Round 2
Problem 21 AMC 10 Daily Practice Round 2
Problem 22 AMC 10 Daily Practice Round 2
Think Academy Powered by ChatGPT