AMC 8 Daily Practice Round 6

Complete problem set with solutions and individual problem pages

Problem 24 Easy

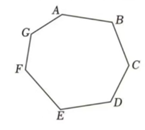
A game piece starts at vertex A of a heptagon board labeled A, B, C, D, E, F, G clockwise. Players move the piece 10 times following this rule: on the k-th move, jump k vertices clockwise. Which vertices remain unvisited after 10 moves?

  • A.

    C, E, and F

  • B.

    E, F

  • C.

    C, E

  • D.

    B,C and F

  • E.

    C, F

Answer:A

Label the vertices as 0 (A), 1 (B), 2 (C), 3 (D), 4 (E), 5 (F), and 6 (G).  

After k moves, the total number of positions traversed is:   S_k = \frac{k(k+1)}{2}  

The final position is determined by computing the remainder Z when S_k is divided by 7:   Z = S_k \bmod 7  

By calculating Z for k=1, 2, \dots, 10, we observe the repeating sequence of remainders:   1, 3, 6, 3, 1, 0, 0, 1, 3, 6.  

Vertices corresponding to remainders 2, 4, and 5 (i.e., C, E, and F) are never visited.  

Final result: \boxed{\text{C, E, and F}}

Related Problems
Problem 22 AMC 8 Daily Practice Round 6
Problem 23 AMC 8 Daily Practice Round 6
Problem 25 AMC 8 Daily Practice Round 6
Problem 26 AMC 8 Daily Practice Round 6
Think Academy Powered by ChatGPT