AMC 10 Daily Practice Round 3
Complete problem set with solutions and individual problem pages
Four regular hexagons surround a square with side length , each one sharing an edge with the square, as shown in the figure below. The area of the resulting -sided outer nonconvex polygon can be written as , where , , and are integers and is not divisible by the square of any prime. What is ?
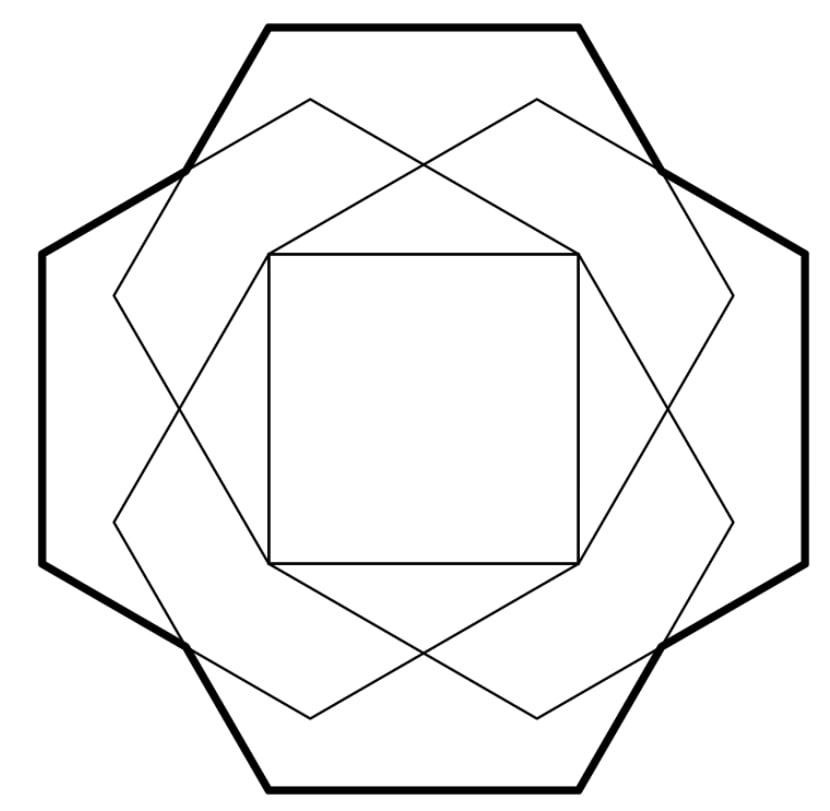
- A.
- B.
- C.
- D.
- E.
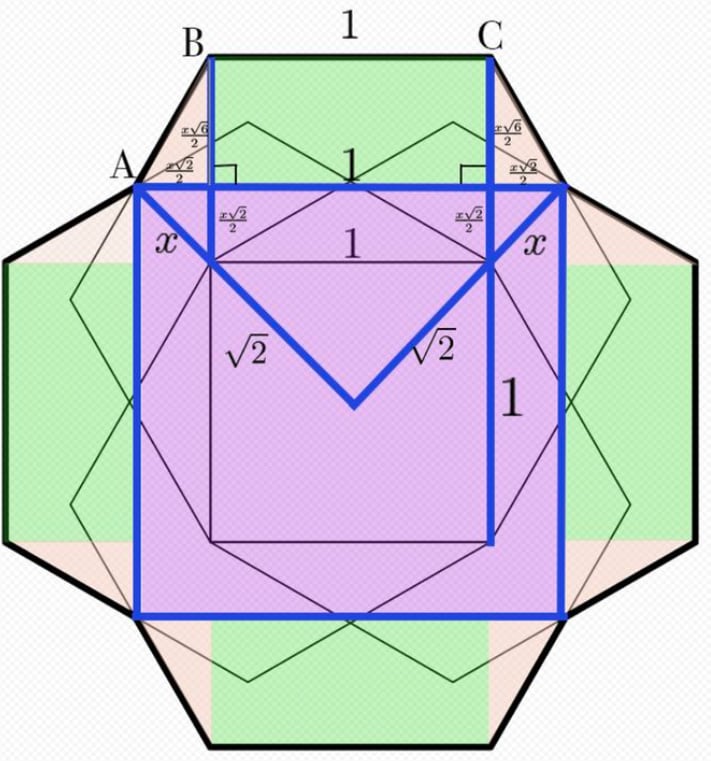
Note that each of the green sections is a rectangle, so its interior angles are all Since , every one of the orange sections is a right triangle.
Define to be the distance from the corner of the square with side length to the corner of the larger blue square. Due to the sides of the two squares being parallel to each other, the large blue triangle is a right triangle. By similarity, the smaller blue triangles are also and have side lengths of and . By triangle relations, the largest altitude of the orange triangle is
Now, we can find the height of the hexagon to obtain an equation in terms of . Consider a hexagon with side length , where point is the foot of the perpendicular dropped from , bisecting :
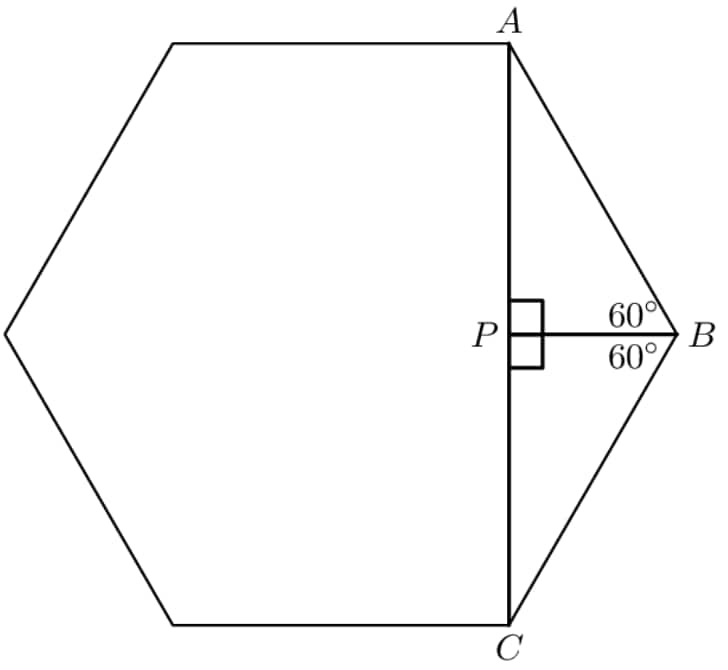
Note that triangles and are congruent -- triangles, by SAS congruence. Since the side length of this hexagon is , the length of is , by -- triangle relations. The height of the hexagon is twice this value, or
The height is also equal to the sum of the values along the long blue line, in the first diagram. Therefore, Solving and rationalizing,
The area of the dodecagon is equal to the sum of the areas of the four rectangles, eight orange triangles, and purple square. In terms of , this is
Plugging in , the area of the dodecagon is . Therefore, the answer is
