2025 AMC 8
Complete problem set with solutions and individual problem pages
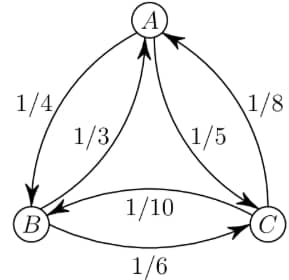
In the land of Markovia, there are three cities: , , and . There are 100 people who live in , 120 who live in , and 160 who live in . Everyone works in one of the three cities, and a person may work in the same city where they live. In the figure below, an arrow pointing from one city to another is labeled with the fraction of people living in the first city who work in the second city. (For example, of the people who live in work in .) How many people work in ?
- A.
- B.
- C.
- D.
- E.
Solution 1
There are people who do not work in city that live in city , meaning that people who live in city work in city . There are people who live in city and work in , as well as people who live in city that work in city . Therefore, the answer is .
Solution 2
We could also make an equation. Let's denote the number of people that live in city as , as , and as . If denotes the number of people working in city , then . This is because of the people from City and of the people from City work in city as shown in the image. We also know that of the people living in work in other cities. We are already given the values of variables , , and as , , and respectively. Plug the values it into the main equation like this: . We solve for it and get our answer .
