AMC 10 Weekly Practice Round 2
Complete problem set with solutions and individual problem pages
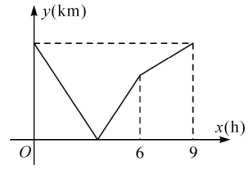
An express train departs from City toward City , while a slow train departs from City toward City . Both trains depart at the same time and stop upon reaching their destinations. Let the travel time of the slow train be hours, and let the distance between the two trains be . The relationship between and is shown in the figure. If the two trains meet at a point that is away from the midpoint between and , then what is the distance between and ?
- A.
- B.
- C.
- D.
- E.
Let the speed of the express train be and the speed of the slow train be . Let the distance between City and City be . From the graph, we know that the express train takes hours to travel the entire distance, and the slow train takes hours. This gives the equation:
Since the two trains meet at a point away from the midpoint between and , we have:
By substituting into the equation:
Solving gives:
Therefore, the answer is .
