2017 AMC 8 Real Questions and Analysis

In this article, you’ll find:

• A concise topic distribution (with a pie chart)
• The core concepts typically tested in each module
• A module-to-question mapping table for the 2017 AMC 8
• Five representative real questions with solutions and common mistakes
• Best resources to prepare for AMC 8

2017 AMC 8 Topic Distribution

The 2017 AMC 8 contains 25 multiple-choice questions completed in 40 minutes, emphasizing logical reasoning and conceptual understanding.

Learn more about AMC 8 Format and Scoring Here: AMC 8 FAQs: The Ultimate Guide for First-Time Test Takers

Detailed Module Analysis

Module	Question Numbers	What It Tests (Brief)
Geometry	6, 11, 16, 18, 22, 25	triangle ratio, square tile diagonals count, perimeters equal triangles, quadrilateral area reasoning, semicircle inscribed geometry, composite region area
Word Problems / Arithmetic	1, 2, 3, 4, 5, 14, 17, 23, 24	expression comparison, percent/pie chart, approximation, large multiplication estimate, fraction product sequence, weighted percent average, count distribution, decreasing speed travel, LCM day count
Number Theory / Algebra	7, 8, 9, 12, 13, 19, 20, 21	repeating digit divisibility, logic statements, minimum color count constraint, modular remainder classification, W-L chess logic inference, factorial divisibility test, 4-digit distinct odd digit probability, a+b+c=0 identity solution set
Combinatorics & Logic	15	counting paths forming AMC8 through adjacency rules
Probability & Statistics	10	random drawing without replacement, largest value probability

Real Questions and Solutions Explained

Geometry Example – Problem 22

Question:

In the right triangle \( \triangle ABC \), \( AC = 12 \), \( BC = 5 \), and \( m{\large \angle}C = 90^\circ \). A semicircle is inscribed in the triangle as shown. What is the radius of the semicircle?

(A) \(\frac{7}{6}\)  (B) \(\frac{13}{5}\)  (C) \(\frac{59}{18}\)  (D) \(\frac{10}{3}\)  (E) \(\frac{60}{13}\)

Solution:

Let the semicircle have center \( O \) on \( AC \) with radius \( r \), tangent to \( BC \) at \( C \) and to \( AB \) at \( D \).
Draw \( OD \) to the tangency point; then \( m{\large \angle}ODB = 90^\circ \).

Quadrilateral \( ODBC \) is a kite, so \( DB = CB = 5 \).
Since \( AB = \sqrt{12^2 + 5^2} = 13 \), we have \( AD = AB – DB = 13 – 5 = 8 \).

Right triangle \( \triangle ADO \) has legs \( AD = 8 \) and \( AO = 12 – r \), and hypotenuse \( OD = r \). Thus

\[
r^2 + 8^2 = (12 – r)^2
\Rightarrow r^2 + 64 = 144 – 24r + r^2
\Rightarrow 24r = 80
\Rightarrow r = \frac{10}{3}.
\]

Answer: (D)

Common Mistakes:

• Treating the semicircle as inscribed only in the hypotenuse and ignoring tangency to \( BC \).
• Using \( AB = 12 + 5 \) instead of \( AB = 13 \) from the Pythagorean theorem.
• Forgetting that \( DB = CB \) from the kite formed by two radii and the tangent.

Word Problem Example – Problem 2

Question:

Alicia, Brenda, and Colby were the candidates in a recent election for student president. The pie chart shows that Brenda received \(30\%\) of the votes. If Brenda received \(36\) votes, how many votes were cast all together?

(A) 70  (B) 84  (C) 100  (D) 106  (E) 120

Solution:

Let the total number of votes be \(x\). Then
\[
\frac{30}{100}\,x = 36
\Rightarrow x = 36\times\frac{100}{30}
= 36\times\frac{10}{3}
= 120.
\]

Answer: (E)

Common Mistakes:

• Treating \(30\%\) as \(0.03\) (i.e., \(\frac{30}{1000}\)).
• Subtracting from 100 instead of solving the proportion.
• Calculator slip when computing \(36\div 0.3\).

Number Theory Example – Problem 19

Question:

For any positive integer \(M\), the notation \(M!\) denotes the product of the integers 1 through \(M\). What is the largest integer \(n\) for which \(5^{n}\) is a factor of the sum \(98!+99!+100!\)?

(A) 23  (B) 24  (C) 25  (D) 26  (E) 27

Solution:

Factor out \(98!\):
\[
98!+99!+100!
=98!\Bigl(1+99+100\cdot99\Bigr)
=98!\cdot10000
=98!\cdot10^{4}.
\]
Therefore
\[
v_{5}\bigl(98!+99!+100!\bigr)=v_{5}(98!)+4.
\]
Compute \(v_{5}(98!)\):
\[
\left\lfloor\frac{98}{5}\right\rfloor
+\left\lfloor\frac{98}{25}\right\rfloor
+\left\lfloor\frac{98}{125}\right\rfloor
=19+3+0=22.
\]
So the exponent of 5 is \(22+4=26\).

Answer: (D)

Common Mistakes:

• Factoring as \(98!(1+99+100)\) and missing the \(100\cdot99\) term.
• Forgetting the extra \(10^{4}\) contributes four factors of 5.
• Miscounting \(v_{5}(98!)\) by omitting the \(\left\lfloor\frac{98}{25}\right\rfloor\) term.

Combinatorics Example – Problem 15

Question:

In the arrangement of letters and numerals below, by how many different paths can one spell AMC8? Beginning at the \(A\) in the middle, a path allows moves only to adjacent cells (up, down, left, or right; no diagonals).

(A) 8  (B) 9  (C) 12  (D) 24  (E) 36

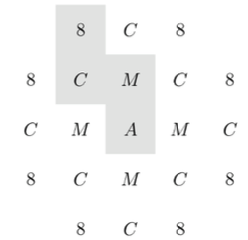
Solution:

From the center \(A\), there are \(4\) adjacent \(M\) cells.
From each \(M\), there are \(3\) adjacent \(C\) cells (not backtracking to \(A\)).
From each \(C\), there are \(2\) adjacent \(8\) cells.

Total paths:
\[
1\times4\times3\times2=24.
\]

Answer: (D)

Common Mistakes:

• Allowing diagonal moves.
• Double-counting by returning to a cell just visited.
• Assuming the same branching number at every step without checking the diagram.

Probability Example – Problem 10

Question:

A box contains five cards, numbered \(1,2,3,4,5\). Three cards are selected randomly without replacement from the box. What is the probability that \(4\) is the largest value selected?

(A) \(\frac{1}{10}\)  (B) \(\frac{1}{5}\)  (C) \(\frac{3}{10}\)  (D) \(\frac{2}{5}\) (E) \(\frac{1}{2}\)

Solution:

\[
\frac{5!}{3!\,2!}=10.
\]
For \(4\) to be the largest, include \(4\) and exclude \(5\); choose the other 2 from \(\{1,2,3\}\):
\[
\frac{3!}{2!\,1!}=3.
\]
Therefore the probability is
\[
\frac{3}{10}.
\]

Answer: (C)

Common Mistakes :

• Forgetting to exclude \(5\).
• Counting ordered draws instead of combinations.
• Using \( \frac{1}{5} \) by thinking only “include 4” without the size-3 constraint.

Best Resources to Prepare for AMC 8

Visit All-in-one AMC8 Resource Hub: past papers, mock tests, and expert walkthroughs

Recommended Reading

• 2018 AMC 8 Real Questions and Analysis
• How to Prepare for AMC 8 Math Competition
• All About 2026 AMC 8: Dates, Registration, Scores and Prep Tips
• AMC 8 FAQs: The Ultimate Guide for First-Time Test Takers

About Think Academy

Think Academy, a top math education brand under TAL Education Group, offers specialized training for the prestigious AMC 8 competition. In 2025, 672 Think Academy students earned national awards—65% of them placed on the Achievement, Honor, or Distinguished Honor Rolls. From 2022 to 2025, our results have grown rapidly, setting records in award counts and perfect scores. Backed by expert teachers and a proven curriculum, Think Academy prepares middle schoolers for lasting success in competitive math. Explore our AMC 8 courses and start your child’s winning journey.

Want more insights on math education and parenting tips? Subscribe to our newsletter for weekly expert advice and updates on the latest learning tools.